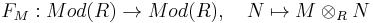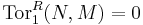Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original sequence is exact.
Vector spaces over a field are flat modules. Free modules, or more generally projective modules, are also flat, over any R. For finitely generated modules over a Noetherian local ring, flatness, projectivity, and freeness are all equivalent.
Flatness was introduced by Serre (1956) in his paper Géometrie Algébrique et Géométrie Analytique. See also flat morphism.
Contents |
Definition
Commutative rings
There are many ways to define flatness over a commutative ring  .
.
- A flat
 -module is an
-module is an  -module
-module  such that the functor
such that the functor
is exact, where 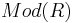 is the category of
is the category of  -modules.
-modules.
- A flat
 -module is an
-module is an  -module
-module  such that for every injective morphism
such that for every injective morphism 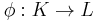 of
of  -modules
-modules  and
and  , the induced map,
, the induced map,
-
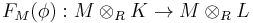 ,
,
is injective.
- A flat
 -module is an
-module is an  -module
-module  such that for every finitely generated ideal
such that for every finitely generated ideal 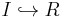 , the induced morphism
, the induced morphism 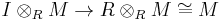 is injective.
is injective. - A flat
 -module is an
-module is an  -module
-module  such that there exists a directed system of
such that there exists a directed system of  -modules
-modules 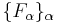 with the following properties:
with the following properties:
- For all
 ,
, 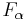 is a finitely generated, free
is a finitely generated, free  -module.
-module. - The direct limit is
 :
: 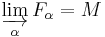 .
.
- A flat
 -module is an
-module is an  -module
-module  such that for every linear dependency in
such that for every linear dependency in  ,
,
-
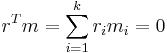 ,
,
where 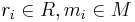 , there exists a matrix
, there exists a matrix 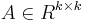 such that
such that
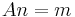 has a solution for some
has a solution for some 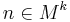 .
.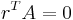 .
.
- A flat
 -module is an
-module is an  -module
-module  such that for every
such that for every  -module
-module  ,
,
- A flat
 -module is an
-module is an  -module
-module  such that for every finitely generated ideal
such that for every finitely generated ideal 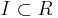 ,
,
-
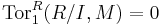 .
.
- A flat
 -module is an
-module is an  -module
-module  such that for every map
such that for every map  , where
, where  is a finitely generated free
is a finitely generated free  -module, and for every finitely generated
-module, and for every finitely generated  -submodule
-submodule 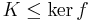 ,
,  factors through a map to a free
factors through a map to a free  -module
-module  that kills
that kills  :
:
General rings
When R isn't commutative one needs the more careful statement, that (if M is a left R-module) the tensor product with M maps exact sequences of right R-modules to exact sequences of abelian groups.
Taking tensor products (over arbitrary rings) is always a right exact functor. Therefore, the R-module M is flat if and only if for any injective homomorphism K → L of R-modules, the induced homomorphism K M → L
M → L M is also injective.
M is also injective.
Case of commutative rings
For any multiplicatively closed subset S of R, the localization ring 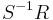 is flat as an R-module.
is flat as an R-module.
When R is Noetherian and M is a finitely-generated R-module, being flat is the same as being locally free in the following sense: M is a flat R-module if and only if for every prime ideal (or even just for every maximal ideal) P of R, the localization 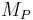 is free as a module over the localization
is free as a module over the localization 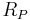 .
.
If S is an R-algebra, i.e., we have a homomorphism 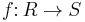 , then S has the structure of an R-module, and hence it makes sense to ask if S is flat over R. If this is the case, then S is faithfully flat over R if and only if every prime ideal of R is the inverse image under f of a prime ideal in S. In other words, if and only if the induced map
, then S has the structure of an R-module, and hence it makes sense to ask if S is flat over R. If this is the case, then S is faithfully flat over R if and only if every prime ideal of R is the inverse image under f of a prime ideal in S. In other words, if and only if the induced map 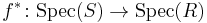 is surjective.
is surjective.
Categorical colimits
In general, arbitrary direct sums and direct limits of flat modules are flat, a consequence of the fact that the tensor product commutes with direct sums and direct limits (in fact with all colimits), and that both direct sums and direct limits are exact functors. Submodules and factor modules of flat modules need not be flat in general. However we have the following result: the homomorphic image of a flat module M is flat if and only if the kernel is a pure submodule of M.
Daniel Lazard proved in 1969 that a module M is flat if and only if it is a direct limit of finitely-generated free modules. As a consequence, one can deduce that every finitely-presented flat module is projective.
An abelian group is flat (viewed as a Z-module) if and only if it is torsion-free.
Homological algebra
Flatness may also be expressed using the Tor functors, the left derived functors of the tensor product. A left R-module M is flat if and only if TornR(–, M) = 0 for all 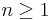 (i.e., if and only if TornR(X, M) = 0 for all
(i.e., if and only if TornR(X, M) = 0 for all 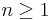 and all right R-modules X). Similarly, a right R-module M is flat if and only if TornR(M, X) = 0 for all
and all right R-modules X). Similarly, a right R-module M is flat if and only if TornR(M, X) = 0 for all 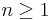 and all left R-modules X. Using the Tor functor's long exact sequences, one can then easily prove facts about a short exact sequence
and all left R-modules X. Using the Tor functor's long exact sequences, one can then easily prove facts about a short exact sequence
- If A and C are flat, then so is B
- If B and C are flat, then so is A
If A and B are flat, C need not be flat in general. However, it can be shown that
- If A is pure in B and B is flat, then A and C are flat.
Flat resolutions
A flat resolution of a module is a resolution by flat modules. Any projective resolution is therefore a flat resolution. These flat resolutions can also be used to compute the Tor functor.
In some areas of module theory, a flat resolution must satisfy the additional requirement that each map is a flat pre-cover of the kernel of the map to the right. For projective resolutions, this condition is almost invisible: a projective pre-cover is simply an epimorphism from a projective module. These ideas are inspired from Auslander's work in approximations. These ideas are also familiar from the more common notion of minimal projective resolutions, where each map is required to be a projective cover of the kernel of the map to the right. However, projective covers need not exist in general, so minimal projective resolutions are only of limited use over rings like the integers.
While projective covers for modules do not always exist, it was speculated that for general rings, every module would have a flat cover, that is, every module would be the epimorphic image of a flat module under a homomorphism with superfluous kernel. This flat cover conjecture was explicitly first stated in (Enochs 1981, p.196). The conjecture turned out to be true, resolved positively and proved simultaneously by L. Bican, R. El Bashir and E. Enochs (see (Bichan-El Bashir-Enochs 2001)). The was preceded by important contributions by P. Eklof, J. Trlifaj and J. Xu.
Since flat covers exist for all modules over all rings, minimal flat resolutions can take the place of minimal projective resolutions in many circumstances. The measurement of the departure of flat resolutions from projective resolutions is called relative homological algebra, and is covered in classics such as (MacLane 1963) and in more recent works focussing on flat resolutions such as (Enochs & Jenda 2000).
In constructive mathematics
Flat modules have increased importance in constructive mathematics, where projective modules are less useful. For example, that all free modules are projective is equivalent to the full axiom of choice, so theorems about projective modules, even if proved constructively, do not necessarily apply to free modules. In contrast, no choice is needed to prove that free modules are flat, so theorems about flat modules can still apply, (Richman 1997).
References
- Bican, L.; El Bashir, R.; Enochs, E. (2001), "All modules have flat covers", Bull. London Math. Soc. 33 (4): 385–390, doi:10.1017/S0024609301008104, ISSN 0024-6093, MR1832549
- Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1; 978-0-387-94269-8, MR1322960
- Enochs, Edgar E. (1981), "Injective and flat covers, envelopes and resolvents", Israel J. Math. 39 (3): 189–209, doi:10.1007/BF0276084, ISSN 0021-2172, MR(83a:16031) 636889 (83a:16031)
- Enochs, Edgar E.; Jenda, Overtoun M. G. (2000), Relative homological algebra, de Gruyter Expositions in Mathematics, 30, Berlin: Walter de Gruyter & Co., ISBN 978-3-11-016633-0, MR1753146
- Mac Lane, Saunders (1963), Homology, Die Grundlehren der mathematischen Wissenschaften, Bd. 114, Boston, MA: Academic Press, MR0156879
- Northcott, D. G. (1984), Multilinear algebra, Cambridge University Press, ISBN 978-0-521-26269-9 - page 33
- Richman, Fred (1997), "Flat dimension, constructivity, and the Hilbert syzygy theorem", New Zealand Journal of Mathematics 26 (2): 263–273, ISSN 1171-6096, MR1601663
- Serre, Jean-Pierre (1956), "Géométrie algébrique et géométrie analytique", Université de Grenoble. Annales de l'Institut Fourier 6: 1–42, ISSN 0373-0956, MR0082175, http://www.numdam.org/numdam-bin/item?id=AIF_1956__6__1_0
See also
- localization of a module
- flat morphism
- von Neumann regular ring: those rings over which all modules are flat.